Ллгарифмы для экономики
Лезин Г.Д.
Логарифмы для экономики
До шестнадцатого века люди производили вычисления «столбиками». Но с развитием наук, связанных с большими расстояниями, в частности, астрономии, умножать и делить большие числа таким способом стало трудным делом – столбики просто перестали умещаться на листе бумаги.
Тогда учёные пришли к решению – они степенную функцию «вывернули наизнанку» и, создав таким образом логарифм, заменили умножение и деление на более простые сложение и вычитание.
В результате применения логарифмов и их свойствам экспоненциальности сложные расчёты облегчились и их результаты в графическом виде стали более компактными.
Напомним для тех, кто забыл логарифмы. Например, нам надо возвести в квадрат число 25. Можно умножить столбиком 25 на 25 и получить результат 625. Но можно в таблице логарифмов найти логарифм числа 25 и, увеличив его путём сложения в два раза, опять заглянуть в таблицу логарифмов. Там найдём искомый результат – число 625. В этом примере взяты небольшие числа, которые можно перемножить и столбиком, а что делать, если необходимо, например, возводить в степень многозначные числа или перемножать их и делить?
Коротко говоря, появление логарифмов сыграло большую роль в развитии наук. Образно логарифмирование можно сравнить с микроскопом и телескопом, оно подобно им раздвинуло границы познаваемого мира. Именно благодаря логарифмированию возникла термодинамика, которая, начав своё шествие с паровых двигателей, распространилась на химию, атомную и ядерную физику, астрофизику, метеорологию и другие сферы.
Сейчас на очереди проникновение термодинамики в социалогию и экономику. И здесь возникает некоторая проблема, заключающаяся в том, что необходимо учесть специфику социально-экономических систем. Во-первых, здесь элементами систем являются не частицы, а люди с присущими им степенями свободы. Во-вторых, число людей, как элементов системы, несравненно меньше. Для сведения: в газе (воздухе) в одном кубическом сантиметре находится 1019 (миллиард раз по десять миллиардов) молекул, то есть в миллиард раз больше населения Земли.
В экономических системах число их участников может быть как большим, так и совсем маленьким, начиная с одного человека (самозанятого). Поэтому надо разобраться, насколько пригодны к социологии общепринятые сейчас логарифмические ряды, успешно работающие с физическими системами.
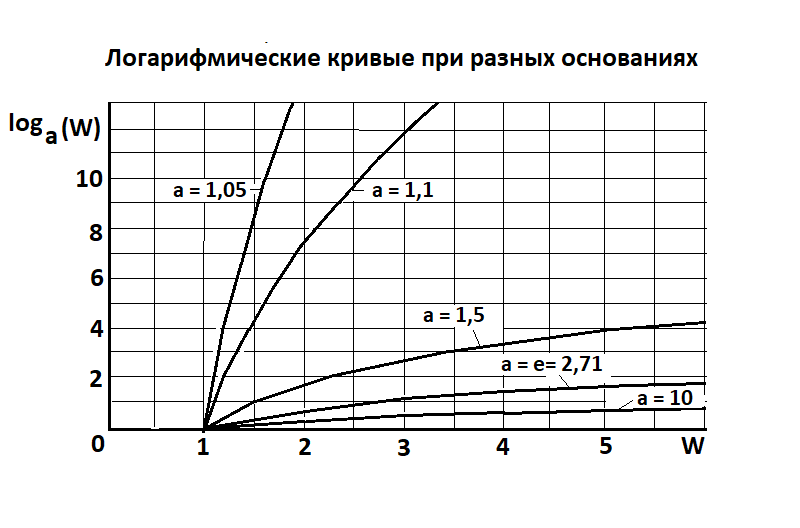
На приведённом выше графике показаны логарифмические кривые, рассчитанные по формуле:
s = loga w , (1)
где: s – логарифм, a – основание логарифма,
W – логарифмируемое число
Исторически первой и применяемой до настоящего времени таблицей логарифмов я вляется «десятичная», созданная на основании a=10. Четыре века назад учёные сочли такое основание логарифмов оптимальным.
Однако позже была создана другая таблица логарифмов, названных «натуральными». К этому был причастен учёный Л.Эйлер, который ввёл в своё время в дифференциальное и интегральное исчисление странное число e=2,7182818284. Д.Бернулли исследовал это число с точки зрения «сложного банковского процента», позволяющего получать дополнительный доход, но не более чем в e раз. Эта логарифмическая система с основанием e прочно вошла в математику, но, кажется, нематематикам безразлично какую таблицу логарифмов использовать для ведения своих расчётов.
Описанные логарифмические ряды с основаниями a=10 и e = 2,718 по всей вероятности могут быть применены и в экономике.
В IXX веке Л.Больцман сформулировал понятие энтропии, опираясь именно на натуральную логарифмическую систему счёта с основанием e. Возникает мысль, не потому ли это произошло, что этот вариант логарифмического изменения численного ряда действительно ближе к природе? Но, как видно из приведённого на рисунке выше семейства логарифмических кривых «натуральный» вариант не является крайним, предельным, явно отличным от других.
Преобразуем выражение (1) в формулу энтропии по Больцману:
S0 = K. lnW0 , (2)
где K – постоянная Больцмана, W0 – термодинамическая вероятность. Очевидно, что большая часть смысловой нагрузки в этой короткой формуле приходится на натуральный логарифм. Тот же вопрос: возможно такое, что натуральный логарифм больше других подобен процессам, протекающим в неживых термодинамических системах, для которых и была создана теория Больцмана?
Если это так, то не стоит ли поискать другую логарифмическую зависимость для описания процессов в социально-экономической сфере? Например, одну из показанных на графике с: а = 1,5; 1,1 или 1,05?
Видимо, ответ на этот вопрос можно будет получить только при проведении практических исследований.
Что касается постоянной Больцмана, в экономическом варианте он должен быть другим, ведь люди не атомы.



